Absorption law

In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.

Two binary operations, say ¤ and *, are said to be connected by the absorption law if:

a ¤ (a * b) = a * (a ¤ b) = a.

A set equipped with two commutative and associative binary operations ∨ ("join") and ∧ ("meet") which are connected by the absorption law

a ∨ (a ∧ b) = a ∧ (a ∨ b) = a

is called a lattice. Examples of lattices include Boolean algebras and Heyting algebras.

In classical logic, and in particular in Boolean algebra, the operations OR and AND, which are also denoted by 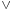$\scriptstyle \lor$ and $\scriptstyle \land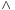$ , also satisfy the lattice axioms, including the absorption law. The same is true for intuitionistic logic.

The commutative and associative laws also hold for addition and multiplication in commutative rings, e.g. in the field of real numbers. The absorption law is the critical property that is missing in this case, since in general a · (a + b) ≠ a and a + (a · b) ≠ a.

The absorption law also fails to hold for relevance logics, linear logics, and substructural logics. In the last case, there is no one-to-one correspondence between the free variables of the defining pair of identities.

References

Davey, B. A., and Priestley, H. A. (2002). Introduction to Lattices and Order (second ed.). Cambridge University Press. ISBN 0-521-78451-4.
Weisstein, Eric W., "Absorption Law" from MathWorld.